(本小题满分12分)在某学校组织的一次篮球定点投篮训练中,规定每人最多投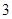 次:在
次:在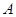 处每投进一球得
处每投进一球得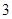 分,在
分,在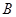 处每投进一球得
处每投进一球得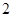 分;如果前两次得分之和超过
分;如果前两次得分之和超过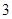 分即停止投篮,否则投第三次.某同学在
分即停止投篮,否则投第三次.某同学在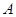 处的命中率
处的命中率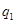 为
为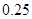 ,在
,在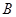 处的命中率为
处的命中率为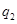 ,该同学选择先在
,该同学选择先在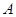 处投一球,以后都在
处投一球,以后都在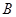 处投,用
处投,用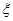 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
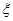 |
0 |
2 |
3 |
4 |
5 |
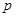 |
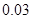 |
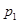 |
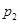 |
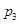 |
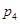 |
(1) 求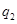 的值;
的值; (2) 求随机变量
(2) 求随机变量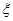 的数学期望
的数学期望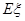 ;
;
(3) 试比较该同学选择都在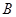 处投篮得分超过
处投篮得分超过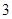 分与选择上述方式投篮得分超过
分与选择上述方式投篮得分超过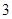 分的概率的大小.
分的概率的大小.
相关知识点
推荐套卷
 .
.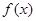 的最小正周期;(2)求函数
的最小正周期;(2)求函数 时,求函数
时,求函数 的值。
的值。 ,
, 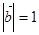
 的夹角
的夹角 为45°,求
为45°,求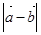

 ,求
,求 的夹角
的夹角 的内角
的内角 的对边
的对边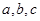 ,
,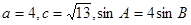 。
。 边的长;(2)求角
边的长;(2)求角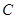 的大小; (3)求
的大小; (3)求 (2)求值
(2)求值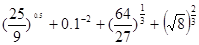

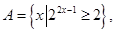
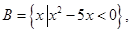 求(1)A∩B,A∪B;
求(1)A∩B,A∪B;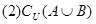
 粤公网安备 44130202000953号
粤公网安备 44130202000953号