（本小题满分12分）
一缉私艇A发现在北偏东
方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南
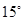方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
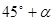的方向去追,.求追及所需的时间和
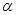角的正弦值.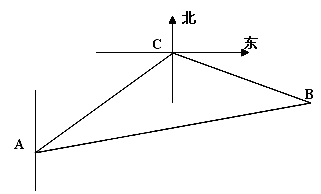
相关试题
ABCD的两条对角线AC与BD交于E，O是任意一点，
+
+
+
=4
所在的平面上有一点
，满足
，则
与
B．
C．
D．
相关知识点
推荐套卷
（本小题满分12分）
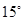一缉私艇A发现在北偏东方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东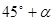的方向去追,.求追及所需的时间和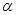角的正弦值.
粤公网安备 44130202000953号