(本小题满分14分)若集合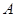 具有以下性质:
具有以下性质:
① ,
, ;
;
②若 ,则
,则 ,且
,且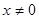 时,
时,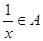 .
.
则称集合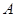 是“好集”.
是“好集”.
(Ⅰ)分别判断集合 ,有理数集
,有理数集 是否是“好集”,并说明理由;
是否是“好集”,并说明理由;
(Ⅱ)设集合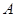 是“好集”,求证:若
是“好集”,求证:若 ,则
,则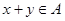 ;
;
(Ⅲ)对任意的一个“好集”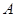 ,
, 分别判断下面命题的真假,并说明理由.
分别判断下面命题的真假,并说明理由.
命题 :若
:若 ,则必有
,则必有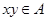 ;
;
命题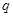 :若
:若
 ,且
,且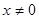 ,则必有
,则必有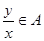 ;
;
推荐套卷
(本小题满分14分)若集合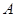 具有以下性质:
具有以下性质:
① ,
, ;
;
②若 ,则
,则 ,且
,且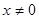 时,
时,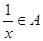 .
.
则称集合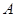 是“好集”.
是“好集”.
(Ⅰ)分别判断集合 ,有理数集
,有理数集 是否是“好集”,并说明理由;
是否是“好集”,并说明理由;
(Ⅱ)设集合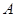 是“好集”,求证:若
是“好集”,求证:若 ,则
,则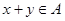 ;
;
(Ⅲ)对任意的一个“好集”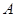 ,
, 分别判断下面命题的真假,并说明理由.
分别判断下面命题的真假,并说明理由.
命题 :若
:若 ,则必有
,则必有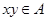 ;
;
命题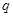 :若
:若
 ,且
,且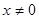 ,则必有
,则必有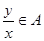 ;
;