如图①所示,已知A、B为直线l上两点,点C为直线l上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1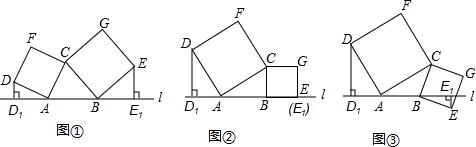
(1)如图②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB;
(2)在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由;
(3)如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系.(不需要证明)
相关知识点
推荐套卷




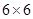 的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.
的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.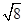 ;
;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号