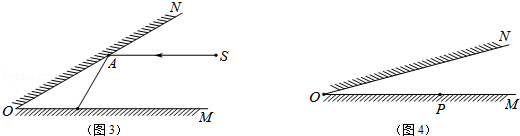我们知道:光反射时,反射光线、入射光线和法线在同一平面内,反射光线、入射光线分别在法线两侧,反射角等于入射角.如右图,
为入射光线,入射点为
,
为法线(过入射点
且垂直于镜面的直线),
为反射光线,此时反射角
等于入射角
.
问题思考:
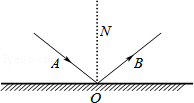
(1)如图1,一束光线从点
处入射到平面镜上,反射后恰好过点
,请在图中确定平面镜上的入射点
,保留作图痕迹,并简要说明理由;
(2)如图2,两平面镜
、
相交于点
,且
,一束光线从点
出发,经过平面镜反射后,恰好经过点
.小昕说,光线可以只经过平面镜
反射后过点
,也可以只经过平面镜
反射后过点
.除了小昕的两种做法外,你还有其它做法吗?如果有,请在图中画出光线的行进路线,保留作图痕迹,并简要说明理由;
问题拓展:
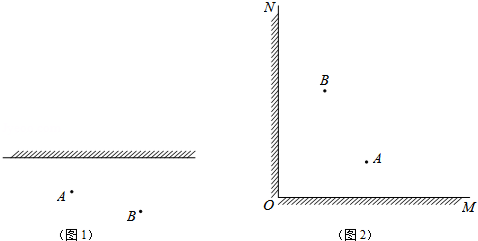
(3)如图3,两平面镜
、
相交于点
,且
,一束光线从点
出发,且平行于平面镜
,第一次在点
处反射,经过若干次反射后又回到了点
,如果
和
的长均为
,求这束光线经过的路程;
(4)如图4,两平面镜
、
相交于点
,且
,一束光线从点
出发,经过若干次反射后,最后反射出去时,光线平行于平面镜
.设光线出发时与射线
的夹角为
,请直接写出满足条件的所有
的度数(注
、
足够长)