如图,在梯形ABCD中, AB∥DC,∠BCD=90°,且AB=1,BC=2,
tan∠ADC=2.
⑴求证:DC=BC;
⑵E是梯形内的一点,F是梯形外的一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;⑶在⑵的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.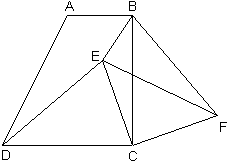
相关知识点
推荐套卷
如图,在梯形ABCD中, AB∥DC,∠BCD=90°,且AB=1,BC=2,
tan∠ADC=2.
⑴求证:DC=BC;
⑵E是梯形内的一点,F是梯形外的一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;⑶在⑵的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.