甲、乙两同学玩“托球赛跑”游戏，商定：用球拍托着乒乓球从起跑线l起跑，绕过P点跑回到起跑线（如图所示）；途中乒乓球掉下时须捡起并回到掉球处继续赛跑，用时少者胜．结果：甲同学由于心急，掉了球，浪费了6秒钟，乙同学则顺利跑完．事后，甲同学说：“我俩所用的全部时间的和为50秒”，乙同学说：“捡球过程不算在内时，甲的速度是我的1.2倍”．根据信息，问哪位同学获胜？（转身拐弯处路程可忽略不计）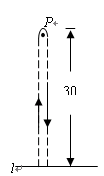
相关试题
甲、乙两同学玩“托球赛跑”游戏，商定：用球拍托着乒乓球从起跑线l起跑，绕过P点跑回到起跑线（如图所示）；途中乒乓球掉下时须捡起并回到掉球处继续赛跑，用时少者胜．结果：甲同学由于心急，掉了球，浪费了6秒钟，乙同学则顺利跑完．事后，甲同学说：“我俩所用的全部时间的和为50秒”，乙同学说：“捡球过程不算在内时，甲的速度是我的1.2倍”．根据信息，问哪位同学获胜？（转身拐弯处路程可忽略不计）
两点在函数
的图象上．
的值及直线
的解析式
，其中
．
中，
，
，求
的长度．
解：
（2）因式分解：
位置的概率是多少？
位置和第四层
解：
粤公网安备 44130202000953号