为从甲、乙两名运动员中选拔一人参加2010年广州亚运会跳水项目，对甲、乙两名运动员进行培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次，得出茎叶图如图所示．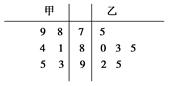
从平均成绩及发挥稳定性的角度考虑，你认为选派哪名运动员合适？
相关试题
．
的图象；
的解集．
，
，且
，求
．
和燃料的质量
、火箭（除燃料外）的质量
的函数关系是
，当燃料质量是火箭质量的 倍时，火箭的最大速度可达12Km/s．
，
，设
．
的定义域及值域；推荐套卷
为从甲、乙两名运动员中选拔一人参加2010年广州亚运会跳水项目，对甲、乙两名运动员进行培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次，得出茎叶图如图所示．
从平均成绩及发挥稳定性的角度考虑，你认为选派哪名运动员合适？
粤公网安备 44130202000953号