（本小题满分12分）
盒内有大小相同的9个球，其中2个红色球，3个白色球，4个黑色球. 规定取出1个红色球得1分，取出1个白色球得0分，取出1个黑色球得－1分 . 现从盒内任取3个球
（Ⅰ）求取出的3个球中至少有一个红球的概率；
（Ⅱ）求取出的3个球得分之和恰为1分的概率；
（Ⅲ）设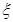
为取出的3个球中白色球的个数，求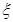的分布列和数学期望.
<
，求实数m的取值范围.
的草图，并求出其单调区间.
的大小.
+
):相关知识点
推荐套卷
（本小题满分12分）
盒内有大小相同的9个球，其中2个红色球，3个白色球，4个黑色球. 规定取出1个红色球得1分，取出1个白色球得0分，取出1个黑色球得－1分 . 现从盒内任取3个球
（Ⅰ）求取出的3个球中至少有一个红球的概率；
（Ⅱ）求取出的3个球得分之和恰为1分的概率；
（Ⅲ）设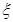为取出的3个球中白色球的个数，求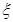的分布列和数学期望.
粤公网安备 44130202000953号