(12分) 一盒中装有分别标记着1，2，3，4的4个小球，每次从袋中取出一只球，设每只小球被取出的可能性相同.
（1）若每次取出的球不放回盒中，现连续取三次球，求恰好第三次取出的球的标号为最大数字的球的概率；
（2）若每次取出的球放回盒中，然后再取出一只球，现连续取三次球，这三次取出的球中标号最大数字为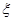
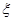，求的分布列与数学期望.
相关试题
与椭圆
有共同的焦点，点
在双曲线C上.
，试求m取何值时
,求使方程有两个大于
的实数根的充要条件。
的图象过点（0，3），且在
和
上为增函数，在
上为减函数.
的解析式；相关知识点
推荐套卷
(12分) 一盒中装有分别标记着1，2，3，4的4个小球，每次从袋中取出一只球，设每只小球被取出的可能性相同.
（1）若每次取出的球不放回盒中，现连续取三次球，求恰好第三次取出的球的标号为最大数字的球的概率；
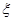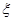（2）若每次取出的球放回盒中，然后再取出一只球，现连续取三次球，这三次取出的球中标号最大数字为，求的分布列与数学期望.
粤公网安备 44130202000953号