如图，将连续的奇数1、3、5、7 …… ，排列成如下的数表，用十字框框出5个数。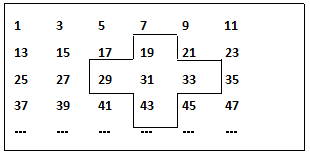
问：(1)十字框框出5个数字的和与框子正中间的数31有什么关系？
(2)若将十字框上下左右平移，可框住另外5个数，若设中间的数为a，用代数式表示十字框框住的5个数字之和；
(3)十字框框住的5个数字之和能等于2000吗？若能，分别写出十字框框住的5个数；若不能，请说明理由。
相关试题
小明家有一块长8
，宽6的矩形空地，妈妈准备在该空地上建造一个花园，并使花园面积为空地面积的一半.小明设计了如下的四种方案供妈妈挑选.请你选择其中的一种方案帮助小明求出图中的
值.
有两个不相等的实数根．
的取值范围；
有一个相同的根，求此时
的值．在平面直角坐标系中，△ABC的顶点坐标是A（-7，1），B（1，1），C（1，7）．线段DE的端点坐标是D（7，-1），E（-1，-7）．
（1）试说明如何平移线段AC，使其与线段ED重合；
（2）将△ABC绕坐标原点O逆时针旋转，使AC的对应边为DE，请直接写出点B的对应点F的坐标；
（3）画出（2）中的△DEF，并和△ABC同时绕坐标原点O逆时针旋转90°，画出旋转后的图形．
粤公网安备 44130202000953号