如图，矩形ABCD的两边长AB=18cm，AD=4cm，点P、Q分别从A、B同时出发，P在边AB上沿AB方向以每秒2cm的速度匀速运动，Q在边BC上沿BC方向以每秒1cm的速度匀速运动．设运动时间为x秒，△PBQ的面积为y（cm2）.
（1）求y关于x的函数关系式，并写出x的取值范围；
（2）求△PBQ的面积的最大值.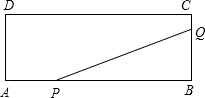
相关试题
．其中
．
；
相关知识点
推荐套卷
如图，矩形ABCD的两边长AB=18cm，AD=4cm，点P、Q分别从A、B同时出发，P在边AB上沿AB方向以每秒2cm的速度匀速运动，Q在边BC上沿BC方向以每秒1cm的速度匀速运动．设运动时间为x秒，△PBQ的面积为y（cm2）.
（1）求y关于x的函数关系式，并写出x的取值范围；
（2）求△PBQ的面积的最大值.
粤公网安备 44130202000953号