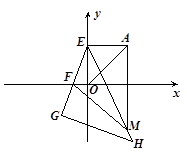如图,在平面直角坐标系中,△AOB为等腰直角三角形,AB=OA,A(4,4)。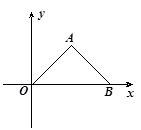
(1)求B点坐标;
(2)若C为x轴正半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°连OD,求∠AOD的度数;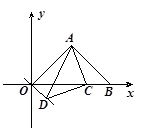
(3)过点A作y轴的垂线交y轴于E,F为x轴负半轴上一点,G在EF的延长线上,以EG为直角边作等腰Rt△EGH,过A作x轴垂线交EH于点M,连FM,等式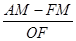 =1是否成立?若成立,请证明:若不成立,说明理由.
=1是否成立?若成立,请证明:若不成立,说明理由.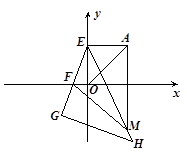
相关知识点
推荐套卷
如图,在平面直角坐标系中,△AOB为等腰直角三角形,AB=OA,A(4,4)。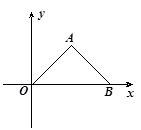
(1)求B点坐标;
(2)若C为x轴正半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°连OD,求∠AOD的度数;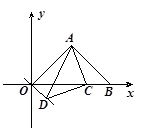
(3)过点A作y轴的垂线交y轴于E,F为x轴负半轴上一点,G在EF的延长线上,以EG为直角边作等腰Rt△EGH,过A作x轴垂线交EH于点M,连FM,等式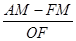 =1是否成立?若成立,请证明:若不成立,说明理由.
=1是否成立?若成立,请证明:若不成立,说明理由.