已知直线 分别与
分别与 轴、
轴、 轴交于点
轴交于点 、
、 ,抛物线
,抛物线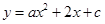 经过点
经过点 、
、 .
.
(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
(2)记该抛物线的对称轴为直线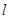 ,点
,点 关于直线
关于直线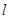 的对称点为
的对称点为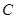 ,若点
,若点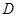 在
在 轴的正半轴上,且四边形
轴的正半轴上,且四边形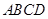 为梯形.
为梯形.
① 求点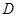 的坐标;
的坐标;
② 将此抛物线向右平移,平移后抛物线的顶点为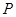 ,其对称轴与直线
,其对称轴与直线 交于点
交于点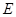 ,若tan
,若tan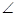
 =
=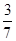 ,求四边形
,求四边形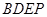 的面积.
的面积.
相关知识点
推荐套卷
已知直线 分别与
分别与 轴、
轴、 轴交于点
轴交于点 、
、 ,抛物线
,抛物线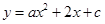 经过点
经过点 、
、 .
.
(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
(2)记该抛物线的对称轴为直线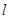 ,点
,点 关于直线
关于直线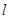 的对称点为
的对称点为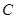 ,若点
,若点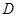 在
在 轴的正半轴上,且四边形
轴的正半轴上,且四边形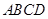 为梯形.
为梯形.
① 求点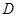 的坐标;
的坐标;
② 将此抛物线向右平移,平移后抛物线的顶点为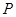 ,其对称轴与直线
,其对称轴与直线 交于点
交于点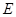 ,若tan
,若tan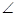
 =
=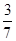 ,求四边形
,求四边形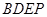 的面积.
的面积.