.(满分12分)某射击比赛,开始时在距目标100米处射击,如果命中记3分,且停止射击;若第一次射击未命中,可以进行第二次射击,但目标已在150米处,这时命中记2分,且停止射击;若第二次仍未命中还可以进行第三次射击,但此时目标已在200米处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分。已知射手在100米处击中目标的概率为 ,他的命中率与目标距离的平方成反比,且各次射击都是独立的。
,他的命中率与目标距离的平方成反比,且各次射击都是独立的。
(1)求这名射手在射击比赛中命中目标的概率;
(2)求这名射手在比赛中得分的数学期望。
相关知识点
推荐套卷
 .
.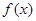 的最小正周期;
的最小正周期;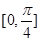 上的函数值的取值范围.
上的函数值的取值范围.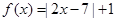 。
。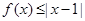 的解集;
的解集;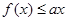 成立,求实数a的取值范围。
成立,求实数a的取值范围。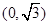 ,曲线C的参数方程为
,曲线C的参数方程为 (φ为参数)。以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(φ为参数)。以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为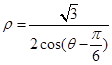 。
。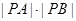 的值。
的值。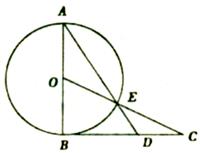
 ,
,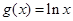 .
. 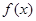 与
与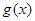 的图象在x = x0处的切线斜率总想等,求x0的值;
的图象在x = x0处的切线斜率总想等,求x0的值;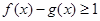 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。 粤公网安备 44130202000953号
粤公网安备 44130202000953号