(本小题满分12分)
如图,已知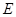 ,
,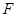 分别是正方形
分别是正方形 边
边 、
、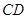 的中点,
的中点,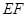 与
与 交于点
交于点 ,
, 、
、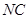 都垂直于平面
都垂直于平面 ,且
,且 ,
,  ,
,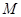 是线段
是线段 上一动点.
上一动点.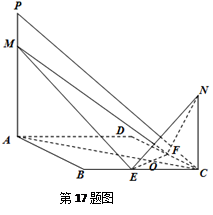
(Ⅰ)求证:平面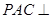 平面
平面 ;
;
(Ⅱ)试确定点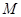 的位置,使得
的位置,使得 平面
平面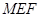 ;
;
(Ⅲ)当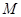 是
是 中点时,求二面角
中点时,求二面角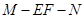 的余弦值.
的余弦值.
推荐套卷
(本小题满分12分)
如图,已知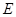 ,
,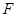 分别是正方形
分别是正方形 边
边 、
、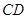 的中点,
的中点,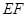 与
与 交于点
交于点 ,
, 、
、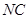 都垂直于平面
都垂直于平面 ,且
,且 ,
,  ,
,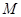 是线段
是线段 上一动点.
上一动点.
(Ⅰ)求证:平面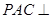 平面
平面 ;
;
(Ⅱ)试确定点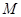 的位置,使得
的位置,使得 平面
平面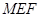 ;
;
(Ⅲ)当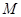 是
是 中点时,求二面角
中点时,求二面角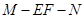 的余弦值.
的余弦值.