（本小题满分14分）
已知函数f(x)的定义域为
，
且同时满足：①f(1)=3；②
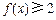对一切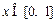
恒成立；③若
，
，
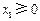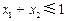，则
．
①求函数f(x)的最大值
和最小值；
②试比较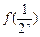
与
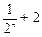
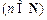的大小；
③某同学发现：当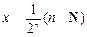
时，有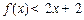
，由此他提出猜想：对一切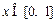，都有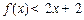，请你判断此猜想是否正确，并说明理由．
相关试题
，点
是双曲线的渐近线与椭圆的一个交点，求双曲线与椭圆的方程。
上求一点，使这点到直线
的距离最短。
个，从中任取
次
求：
的平行线，把一枚半径
的硬币任意掷在这个平面上，求硬币不与任何一条平行线相碰的概率。
颗质地均匀的骰子，求点数和为
的概率推荐套卷
（本小题满分14分）
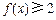已知函数f(x)的定义域为，且同时满足：①f(1)=3；②对一切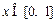恒成立；③若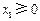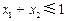，，，则．
①求函数f(x)的最大值和最小值；
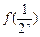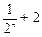
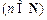②试比较与 的大小；
③某同学发现：当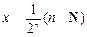时，有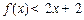，由此他提出猜想：对一切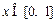，都有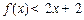，请你判断此猜想是否正确，并说明理由．
粤公网安备 44130202000953号