(Ⅰ)小问5分,(Ⅱ)小问7分)
安排四个大学生到A、B、C三个学校支教,设每个大学生去任何一个学校是等可能的.
(1)求四个大学生中恰有两人去A校支教的概率.
(2)设有大学生去支教的学校的个数为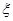 ,求
,求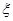 的分布列.
的分布列.
相关知识点
推荐套卷
(Ⅰ)小问5分,(Ⅱ)小问7分)
安排四个大学生到A、B、C三个学校支教,设每个大学生去任何一个学校是等可能的.
(1)求四个大学生中恰有两人去A校支教的概率.
(2)设有大学生去支教的学校的个数为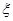 ,求
,求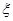 的分布列.
的分布列.