某工厂生产甲、乙两种产品,甲产品的一等品率为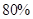 ,二等品率为
,二等品率为 ;乙产品的一等品率为
;乙产品的一等品率为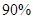 ,二等品率为
,二等品率为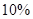 .生产
.生产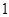 件甲产品,若是一等品,则获利
件甲产品,若是一等品,则获利 万元,若是二等品,则亏损
万元,若是二等品,则亏损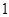 万元;生产
万元;生产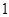 件乙产品,若是一等品,则获利
件乙产品,若是一等品,则获利 万元,若是二等品,则亏损
万元,若是二等品,则亏损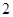 万
万
元.两种产品生产的质量相互独立.
(Ⅰ)设生产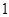 件甲产品和
件甲产品和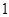 件乙产品可获得的总利润为
件乙产品可获得的总利润为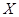 (单位:万元),求
(单位:万元),求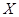 的分布列;
的分布列;
(Ⅱ)求生产 件甲产品所获得的利润不少于
件甲产品所获得的利润不少于 万元的概率.
万元的概率.
相关知识点
推荐套卷
某工厂生产甲、乙两种产品,甲产品的一等品率为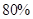 ,二等品率为
,二等品率为 ;乙产品的一等品率为
;乙产品的一等品率为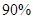 ,二等品率为
,二等品率为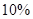 .生产
.生产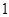 件甲产品,若是一等品,则获利
件甲产品,若是一等品,则获利 万元,若是二等品,则亏损
万元,若是二等品,则亏损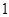 万元;生产
万元;生产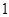 件乙产品,若是一等品,则获利
件乙产品,若是一等品,则获利 万元,若是二等品,则亏损
万元,若是二等品,则亏损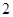 万
万
元.两种产品生产的质量相互独立.
(Ⅰ)设生产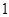 件甲产品和
件甲产品和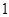 件乙产品可获得的总利润为
件乙产品可获得的总利润为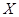 (单位:万元),求
(单位:万元),求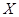 的分布列;
的分布列;
(Ⅱ)求生产 件甲产品所获得的利润不少于
件甲产品所获得的利润不少于 万元的概率.
万元的概率.