如图，在四棱锥P－ABCD中，PA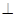
底面ABCD,
DAB为直角，AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
（Ⅰ）试证：CD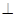平面BEF;
（Ⅱ）设PA＝k·AB,且二面角E-BD-C的平面角大于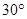
,求k的取值范围.
相关试题
.
，求
的值；
的最大值.
的前n项和为
，已知
，
是
和
的等比中项．
，其中
是函数
的极值点，求
的值；
上的最大值是0，求
是等差数列，其前
项和为
，
是等比数列（
），且
，
为数列
的前
中，内角
所对的边分别为
。已知
的值；
，求相关知识点
推荐套卷
如图，在四棱锥P－ABCD中，PA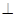底面ABCD,DAB为直角，AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
（Ⅰ）试证：CD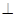平面BEF;
（Ⅱ）设PA＝k·AB,且二面角E-BD-C的平面角大于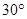,求k的取值范围.
粤公网安备 44130202000953号