2012年6月5日是“世界环境日”，南宁市某校举行了“绿色家园”演讲比赛，赛后整理参赛同学的成绩，制作成直方图（如图）．
（1）分数段在-----范围的人数最多；
（2）全校共有多少人参加比赛？
（3）学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛，并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子．请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果，并求出上衣和能搭配成同一种颜色的概率．
相关试题
、
、
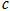在数轴上的位置如图，
化简
（1）3x2＋2x－5x2＋3x
（2）4（m2＋n）＋2（n－2m2）
（3）－3（2x2－xy）－（x2＋xy－6）
（4）－
（6a3b＋2b2）＋
（4a3b－8b2）
（5）先化简，再求值：3x2y－[2x2y－（2xy－3x2y）]＋3xy2，其中x＝3，y＝－
已知抛物线
与
轴交于点
，且
．
（1）求抛物线的解析式．
（2）抛物线的对称轴为
，与y轴的交点为C，顶点为D，点C关于的对称点为E．是否存在x轴上的点M、y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．
（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形
时，求点P的坐标。
相关知识点
推荐套卷
粤公网安备 44130202000953号