如图,在平面直角坐标系xoy中,已知直线l1:y=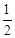 x与直线l2:y=-x+6相交于点M,直线l2与x轴相较于点N.
x与直线l2:y=-x+6相交于点M,直线l2与x轴相较于点N.
求M,N的坐标;
在矩形ABCD中,已知AB=1,BC=2,边AB在x轴上,矩形ABCD沿x轴自左向右以每秒1个
单位长度的速度移动.设矩形ABCD与△OMN的重叠部分的面积为S.移动的时间为t(从点B与点O重合时开始计时,到点A与点N重合时计时结束)。直接写出S与自变量t之间的函数关系式(不需要给出解答过程);
在(2)的条件下,当t为何值时,S的值最大?并求出最大值.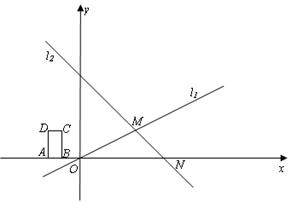
相关知识点
推荐套卷
 分别交
分别交 轴,
轴,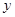 轴于点
轴于点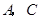 ,点
,点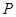 是直线
是直线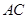 与双曲线
与双曲线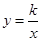 在第一象限内的交点,
在第一象限内的交点,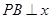 轴,垂足为点
轴,垂足为点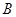 ,
,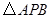 的面积为4.
的面积为4.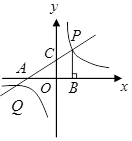
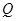 的坐标.
的坐标. 夹角.
夹角.

 .
.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号