(本小题满分13分)
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检査得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如右:
(Ⅰ)若视力测试结果不低于5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(Ⅱ)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求 的分布列及数学期望.
的分布列及数学期望.
相关知识点
推荐套卷
 ,
,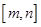 ,
, ,
, 的长度均为
的长度均为 ,其中
,其中 .
.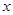 的不等式
的不等式 的解集构成的区间的长度;
的解集构成的区间的长度;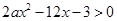 的解集构成的区间的长度为
的解集构成的区间的长度为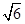 ,求实数
,求实数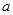 的值;
的值; ,
, 的解集构成的各区间的长度和超过
的解集构成的各区间的长度和超过 ,求实数
,求实数 的取值范围.
的取值范围. ,
, .
.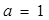 时,求函数
时,求函数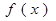 的最大值;
的最大值;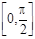 上的任 意一个
上的任 意一个 ,都有
,都有 成立,求
成立,求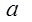 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号