定义区间 ,
,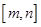 ,
, ,
, 的长度均为
的长度均为 ,其中
,其中 .
.
(1)求关于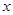 的不等式
的不等式 的解集构成的区间的长度;
的解集构成的区间的长度;
(2)若关于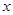 的不等式
的不等式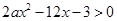 的解集构成的区间的长度为
的解集构成的区间的长度为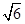 ,求实数
,求实数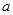 的值;
的值;
(3)已知关于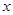 的不等式
的不等式 ,
, 的解集构成的各区间的长度和超过
的解集构成的各区间的长度和超过 ,求实数
,求实数 的取值范围.
的取值范围.
推荐套卷
定义区间 ,
,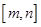 ,
, ,
, 的长度均为
的长度均为 ,其中
,其中 .
.
(1)求关于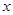 的不等式
的不等式 的解集构成的区间的长度;
的解集构成的区间的长度;
(2)若关于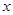 的不等式
的不等式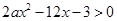 的解集构成的区间的长度为
的解集构成的区间的长度为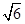 ,求实数
,求实数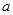 的值;
的值;
(3)已知关于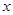 的不等式
的不等式 ,
, 的解集构成的各区间的长度和超过
的解集构成的各区间的长度和超过 ,求实数
,求实数 的取值范围.
的取值范围.