(本小题满分14分)(注意:在试题卷上作答无效)
已知曲线 ,从
,从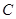 上的点
上的点 作
作 轴的垂线,交
轴的垂线,交 于点
于点 ,再从点
,再从点 作
作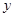 轴的垂线,交
轴的垂线,交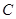 于点
于点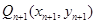 ,设
,设

(1)求数列 的通项公式;
的通项公式;
(2)记 ,数列
,数列 的前
的前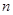 项和为
项和为 ,试比较
,试比较 与
与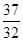 的大小
的大小 ;
;
(3)记 ,数列
,数列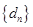 的前
的前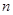 项和为
项和为 ,试证明:
,试证明: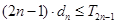

相关知识点
推荐套卷
(本小题满分14分)(注意:在试题卷上作答无效)
已知曲线 ,从
,从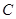 上的点
上的点 作
作 轴的垂线,交
轴的垂线,交 于点
于点 ,再从点
,再从点 作
作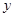 轴的垂线,交
轴的垂线,交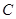 于点
于点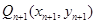 ,设
,设

(1)求数列 的通项公式;
的通项公式;
(2)记 ,数列
,数列 的前
的前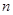 项和为
项和为 ,试比较
,试比较 与
与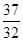 的大小
的大小 ;
;
(3)记 ,数列
,数列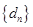 的前
的前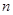 项和为
项和为 ,试证明:
,试证明: