（本小题满分12分）已知函数
（1）讨论函数
的单调性
（2）若函数
与函数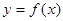
的图像关于原点对称且
就函数分别求解下面两问：
（Ⅰ）问是否存在过点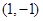
的直线与函数的图象相切？ 若存在，有多少条？若不存在，说明理由
（Ⅱ）求证：对于任意正整数
，均有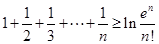
（
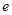为自然对数的底数）
.
）当
时，求曲线
在
处的切线方程（
）
的单调区间。
且
。
的解析式及定义域。
的底面为直角梯形，
，
底面
，且
，
，
是
的中点。
面
；
与
与面
所成二面角的余弦值。
在
内有极值，求实数
的范围。
，
（
为实数且
是虚数单位），求函数
的值域。推荐套卷
（本小题满分12分）已知函数
（1）讨论函数的单调性
（2）若函数与函数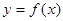的图像关于原点对称且就函数分别求解下面两问：
（Ⅰ）问是否存在过点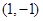的直线与函数的图象相切？ 若存在，有多少条？若不存在，说明理由
（Ⅱ）求证：对于任意正整数，均有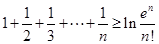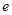（为自然对数的底数）
粤公网安备 44130202000953号