(本小题满分13分)
如图,已知抛物线 ,过点
,过点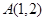 作抛物线
作抛物线 的弦
的弦 ,
,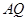 .
.
(Ⅰ)若 ,证明直线
,证明直线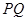 过定点,并求出定点的坐标;
过定点,并求出定点的坐标;
(Ⅱ)假设直线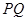 过点
过点 ,请问是否存在以
,请问是否存在以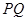 为底边的等腰三角形
为底边的等腰三角形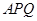 ? 若存在,求出
? 若存在,求出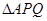 的个数?如果不存在,请说明理由.
的个数?如果不存在,请说明理由.
相关知识点
推荐套卷
(本小题满分13分)
如图,已知抛物线 ,过点
,过点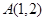 作抛物线
作抛物线 的弦
的弦 ,
,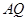 .
.
(Ⅰ)若 ,证明直线
,证明直线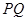 过定点,并求出定点的坐标;
过定点,并求出定点的坐标;
(Ⅱ)假设直线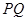 过点
过点 ,请问是否存在以
,请问是否存在以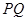 为底边的等腰三角形
为底边的等腰三角形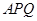 ? 若存在,求出
? 若存在,求出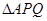 的个数?如果不存在,请说明理由.
的个数?如果不存在,请说明理由.