已知椭圆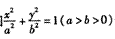 长轴上有一点到两个焦点之间的距离分别为:3+2
长轴上有一点到两个焦点之间的距离分别为:3+2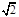 ,3-2
,3-2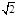
(1)求椭圆的方程;
(2)如果直线x=t(teR)与椭圆相交于A,B,若C(-3,0),D(3,0),证明直线CA与直线
BD的交点K必在一条确定的双曲线上;
(3)过点Q(1,0 )作直线l(与x轴不垂直)与椭圆交于M,N两点,与y轴交于点R,、若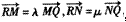 ,求证:
,求证: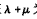 为定值.
为定值.
推荐套卷
已知椭圆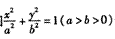 长轴上有一点到两个焦点之间的距离分别为:3+2
长轴上有一点到两个焦点之间的距离分别为:3+2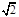 ,3-2
,3-2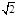
(1)求椭圆的方程;
(2)如果直线x=t(teR)与椭圆相交于A,B,若C(-3,0),D(3,0),证明直线CA与直线
BD的交点K必在一条确定的双曲线上;
(3)过点Q(1,0 )作直线l(与x轴不垂直)与椭圆交于M,N两点,与y轴交于点R,、若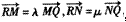 ,求证:
,求证: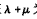 为定值.
为定值.