为了了解本校2014-2015学年七年级学生的身体素质情况,体育老师随机抽取了本校50名2014-2015学年七年级学生进行一分钟跳绳次数测试,测试所得样本数据(单位:次)如下:
88 90 92 96 99 102 106 108 110 112
113 115 115 117 118 120 120 123 125 127
130 132 134 134 134 135 136 137 138 138
139 141 142 142 143 144 145 146 148 149
150 152 153 157 160 162 162 165 168 172
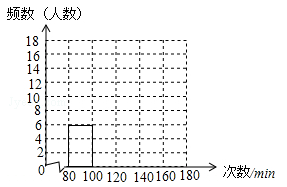
(1)记跳绳次数为x,补全下面的样本频数分布表与频数分布直方图:
组别
|
次数(x)
|
频数(人数)
|
1
|
80≤x<100
|
5
|
2
|
100≤x<120
|
|
3
|
120≤x<140
|
|
4
|
140≤x<160
|
|
5
|
160≤x<180
|
|
(2)若该年级有300名学生,请根据样本数据估计该校2014-2015学年七年级学生中一分钟跳绳次数不低于120次的学生大约有多少人?