（本小题满分14分）
在一个半径为1的半球材料中截取三个高度均为h的圆柱，其轴截面如图所示，设三个圆柱体积之和为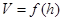
。
（１） 求f(h)的表达式，并写出h的取值范围是 ；
（２） 求三个圆柱体积之和V的最大值；
，请你画出用纸片盖住的三角形．
，请你在线段上表示出来．
相关知识点
推荐套卷
（本小题满分14分）
在一个半径为1的半球材料中截取三个高度均为h的圆柱，其轴截面如图所示，设三个圆柱体积之和为。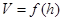
（１） 求f(h)的表达式，并写出h的取值范围是 ；
（２） 求三个圆柱体积之和V的最大值；
粤公网安备 44130202000953号