(本小题满分13分)
已知定义在R上的函数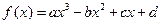
(a，b，c，d为实常数)的图象关于原点对称，且当x＝1时f(x)取得极值
.
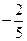（Ⅰ）求函数f(x)的解析式；
（Ⅱ）证明：对任意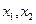
∈[－1，1]，不等式
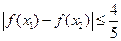成立；
（Ⅲ）若函数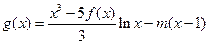
在区间(1，∞)内无零点，求实数m的取值范围.
相关试题
是以点
为圆心，
为半径的圆．
所截得的弦长．
，求矩阵
．
有且仅有两个极值点
．
的取值范围；
？如存在，求
的极大值；如不存在，请说明理由．
是等差数列，
是等比数列，且满足
，
．
，
．
时，求数列
的值；
，
，
均为正整数，且成等比数列，求数列
的最大值．推荐套卷
(本小题满分13分)
已知定义在R上的函数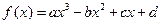(a，b，c，d为实常数)的图象关于原点对称，且当x＝1时f(x)取得极值.
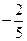（Ⅰ）求函数f(x)的解析式；
（Ⅱ）证明：对任意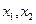∈[－1，1]，不等式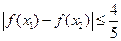成立；
（Ⅲ）若函数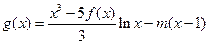在区间(1，∞)内无零点，求实数m的取值范围.
粤公网安备 44130202000953号