已知{an}为递增的等比数列，且{a1，a3，a5}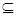
{－10，－6，－2,0,1,3,4,16}．
(1)求数列{an}的通项公式；
(2)是否存在等差数列{bn}，使得a1bn＋a2bn－1＋a3bn－2＋…＋anb1＝2n+1－n－2对一切n∈N*都成立？若存在，求出bn；若不存在，说明理由．
相关试题
或
，分别求满足下列条件的实数m的取值范围：
的最小值；
．
，写出数列
的前5项；
．
方程
有两个不等的正实数根，命题
方程
无实数根。若“
或
”为真命题，求
的取值范围。相关知识点
推荐套卷
已知{an}为递增的等比数列，且{a1，a3，a5}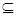{－10，－6，－2,0,1,3,4,16}．
(1)求数列{an}的通项公式；
(2)是否存在等差数列{bn}，使得a1bn＋a2bn－1＋a3bn－2＋…＋anb1＝2n+1－n－2对一切n∈N*都成立？若存在，求出bn；若不存在，说明理由．
粤公网安备 44130202000953号