如图所示,某市政府决定在以政府大楼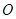 为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径
为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径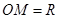 ,
,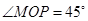 ,
,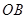 与
与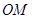 之间的夹角为
之间的夹角为 .
.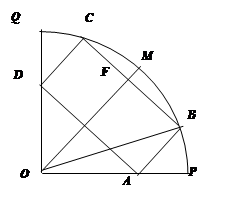
(1)将图书馆底面矩形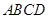 的面积
的面积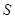 表示成
表示成 的函数.
的函数.
(2)求当 为何值时,矩形
为何值时,矩形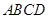 的面积
的面积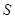 有最大值?
有最大值?
(3)其最大值是多少?(用含R的式子表示)
推荐套卷
如图所示,某市政府决定在以政府大楼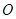 为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径
为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径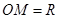 ,
,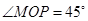 ,
,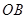 与
与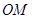 之间的夹角为
之间的夹角为 .
.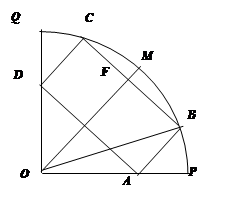
(1)将图书馆底面矩形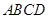 的面积
的面积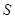 表示成
表示成 的函数.
的函数.
(2)求当 为何值时,矩形
为何值时,矩形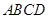 的面积
的面积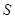 有最大值?
有最大值?
(3)其最大值是多少?(用含R的式子表示)