(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线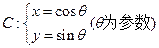 。
。
(Ⅰ)将曲线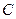 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)若把曲线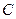 上各点的坐标经过伸缩变换
上各点的坐标经过伸缩变换 后得到曲线
后得到曲线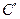 ,求曲线
,求曲线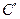 上任意一点到两坐标轴距离之积的最大值.
上任意一点到两坐标轴距离之积的最大值.
相关知识点
推荐套卷
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线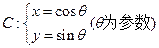 。
。
(Ⅰ)将曲线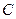 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)若把曲线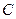 上各点的坐标经过伸缩变换
上各点的坐标经过伸缩变换 后得到曲线
后得到曲线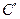 ,求曲线
,求曲线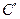 上任意一点到两坐标轴距离之积的最大值.
上任意一点到两坐标轴距离之积的最大值.