(满分12分)已知向量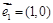 ,
, ,动点
,动点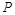 从点
从点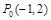 开始沿着与向量
开始沿着与向量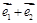 相同的方向做匀速直线运动,速度大小为
相同的方向做匀速直线运动,速度大小为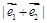 ;另一动点
;另一动点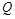 从点
从点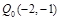 开始沿着与向量
开始沿着与向量 相同的方向做匀速直线运动,速度大小为
相同的方向做匀速直线运动,速度大小为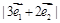 ,设
,设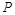 、
、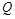 在
在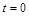 秒时刻分别在
秒时刻分别在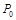 、
、 处.
处.
(Ⅰ)经过多长时间 最小?求出最小值;
最小?求出最小值;
(Ⅱ)经过多长时间后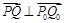 ,求出
,求出 值.
值.
推荐套卷
(满分12分)已知向量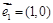 ,
, ,动点
,动点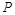 从点
从点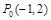 开始沿着与向量
开始沿着与向量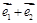 相同的方向做匀速直线运动,速度大小为
相同的方向做匀速直线运动,速度大小为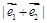 ;另一动点
;另一动点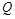 从点
从点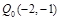 开始沿着与向量
开始沿着与向量 相同的方向做匀速直线运动,速度大小为
相同的方向做匀速直线运动,速度大小为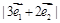 ,设
,设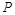 、
、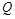 在
在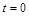 秒时刻分别在
秒时刻分别在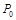 、
、 处.
处.
(Ⅰ)经过多长时间 最小?求出最小值;
最小?求出最小值;
(Ⅱ)经过多长时间后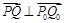 ,求出
,求出 值.
值.