已知反比例函数 图象的两个分支分别位于第一、第三象限.
图象的两个分支分别位于第一、第三象限.
(1)求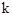 的取值范围;
的取值范围;
(2)若一次函数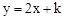 的图象与该反比例函数的图象有一个交点的纵坐标是4.
的图象与该反比例函数的图象有一个交点的纵坐标是4.
①求当 时反比例函数
时反比例函数 的值;
的值;
②当 时,求此时一次函数
时,求此时一次函数 的取值范围.
的取值范围.
相关知识点
推荐套卷
已知反比例函数 图象的两个分支分别位于第一、第三象限.
图象的两个分支分别位于第一、第三象限.
(1)求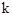 的取值范围;
的取值范围;
(2)若一次函数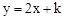 的图象与该反比例函数的图象有一个交点的纵坐标是4.
的图象与该反比例函数的图象有一个交点的纵坐标是4.
①求当 时反比例函数
时反比例函数 的值;
的值;
②当 时,求此时一次函数
时,求此时一次函数 的取值范围.
的取值范围.