如图(1)，点A、B、C在同一直线上，且△ABE, △BCD都是等边三角形，连结AD,CE.
(1)△BEC可由△ABD顺时针旋转得到吗？若是，请描述这一旋转变换过程；若不是，请说明理由；
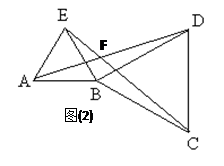
(2)若△BCD绕点B顺时针旋转，使点A,B,C不在同一直线上（如图(2)），则在旋转过程中:
①线段AD与EC的长度相等吗？请说明理由．
②锐角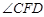
的度数是否改变？若不变，请求出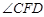的度数；若改变，请说明理由.
(注:等边三角形的三条边都相等,三个角都是60°)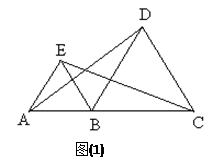
相关试题
如图，在方格纸中，△ABC的三个顶点和点P都在小方格的顶点上，按要求画一个三角形，使它的顶点在方格的顶点上。
（1）将△ABC平移，使点P落在平移后的三角形内部，在图甲中画出示意图；
（2）以点C为旋转中心，将△ABC旋转，使点P落在旋转后的三角形内部，在图乙中画出示意图。
如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB，于点E
（1）求证：△ACD≌△AED；
（2）若∠B=30°，CD=1，求BD的长。
；
相关知识点
推荐套卷
粤公网安备 44130202000953号