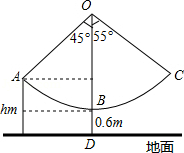
某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳 的长为 ,静止时,踏板到地面距离 的长为 (踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为 ,成人的“安全高度”为 (计算结果精确到
(1)当摆绳 与 成 夹角时,恰为儿童的安全高度,则
(2)某成人在玩秋千时,摆绳 与 的最大夹角为 ,问此人是否安全?(参考数据: , , ,
相关知识点
推荐套卷
某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳 的长为 ,静止时,踏板到地面距离 的长为 (踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为 ,成人的“安全高度”为 (计算结果精确到
(1)当摆绳 与 成 夹角时,恰为儿童的安全高度,则
(2)某成人在玩秋千时,摆绳 与 的最大夹角为 ,问此人是否安全?(参考数据: , , ,
