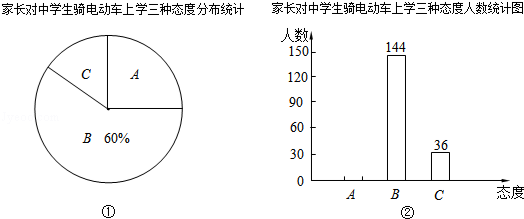
中学生骑电动车上学的现象越来越受到社会的关注．某市记者随机调查了一些家长对这种现象的态度（A：无所谓；B：反对；C：赞成），并将调査结果绘制成图①和图②的统计图（不完整）．请根据图中提供的信息，解答下列问题：
（1）在图①中，C部分所占扇形的圆心角度数为 °；选择图①进行统计的优点是 ；
（2）将图②补充完整；
（3）根据抽样调查结果，请你估计该市50000名中学生家长中有多少名家长持赞成态度？
相关试题
为了增强环境保护意识，6月5日“世界环境日”当天，在环保局工作人员指导下，若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组，抽样调查了全市40个噪声测量点在某时刻的噪声声级（单位：dB），将调查的数据进行处理（设所测数据是正整数），得频数分布表如下：
| 组别 |
噪声声级分组 |
频数 |
频率 |
| 1 |
44.5﹣﹣59.5 |
4 |
0.1 |
| 2 |
59.5﹣﹣74.5 |
a |
0.2 |
| 3 |
74.5﹣﹣89.5 |
10 |
0.25 |
| 4 |
89.5﹣﹣104.5 |
b |
c |
| 5 |
104.5﹣119.5 |
6 |
0.15 |
| 合 计 |
40 |
1.00 |
根据表中提供的信息解答下列问题：
（1）频数分布表中的a=，b=，c=；
（2）补充完整频数分布直方图；
（3）如果全市共有200个测量点，那么在这一时刻噪声声级小于75dB的测量点约有多少个？
，并把它的解集在数轴上表示出来．
，其中m=﹣2．相关知识点
推荐套卷
粤公网安备 44130202000953号