已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上以每秒1个单位的速度由C向B运动。
(1) 求梯形ODPC的面积S与时间t的函数关系式。
(2) t为何值时,四边形PODB是平行四边形?
(3) 在线段PB上是否存在一点Q,使得ODQP为菱形。若存在求t值,若不存在,说明理由。
(4) 当△OPD为等腰三角形时,求点P的坐标。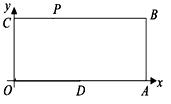
相关知识点
推荐套卷
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上以每秒1个单位的速度由C向B运动。
(1) 求梯形ODPC的面积S与时间t的函数关系式。
(2) t为何值时,四边形PODB是平行四边形?
(3) 在线段PB上是否存在一点Q,使得ODQP为菱形。若存在求t值,若不存在,说明理由。
(4) 当△OPD为等腰三角形时,求点P的坐标。