丽水市在规划新城期间，欲拆除瓯江岸边的一根电线杆AB(如图)，已知距电线杆AB水平距离14米处是河岸，即BD＝14米，该河岸的坡面CD的坡角∠CDF的正切值为2（即tan∠CDF=2），岸高CF为2米，在坡顶C处测得杆顶A的仰角为30°，D、E之间是宽2米的人行道，请你通过计算说明在拆除电线杆AB时，为确保安全，是否将此人行道封上？(在地面上以点B为圆心，以AB长为半径的圆形区域为危险区域)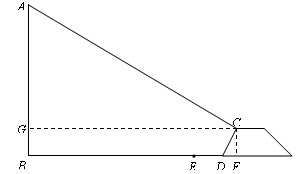
相关试题
（2）
其中
，
.
时，求多项式
的值”，马小虎做题时把
错抄成
，王小真没抄错题，但他们做出的结果却都一样，你知道这是怎么回事吗？说明理由．相关知识点
推荐套卷
粤公网安备 44130202000953号