.如图,在直角坐标系中,点A是反比例函数y1= 的图象上一点,AB⊥x轴的正半轴于点B,C是OB的中点,一次函数y2=ax+b的图象经过A、C两点,并交y轴于点D(0,-2),若S△AO D=4
的图象上一点,AB⊥x轴的正半轴于点B,C是OB的中点,一次函数y2=ax+b的图象经过A、C两点,并交y轴于点D(0,-2),若S△AO D=4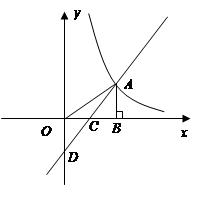
(1)求反比例函数和一次函数解析式。
(2)观察图象,请指出在y轴的右侧,当y1>y2时x 的取值范围
推荐套卷
.如图,在直角坐标系中,点A是反比例函数y1= 的图象上一点,AB⊥x轴的正半轴于点B,C是OB的中点,一次函数y2=ax+b的图象经过A、C两点,并交y轴于点D(0,-2),若S△AO D=4
的图象上一点,AB⊥x轴的正半轴于点B,C是OB的中点,一次函数y2=ax+b的图象经过A、C两点,并交y轴于点D(0,-2),若S△AO D=4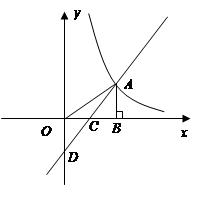
(1)求反比例函数和一次函数解析式。
(2)观察图象,请指出在y轴的右侧,当y1>y2时x 的取值范围