某养鸡场计划购买甲、乙两种小鸡苗共2 000只进行饲养,已知甲种小鸡苗每只2元,乙种小鸡苗每只3元.
(1)若购买这批小鸡苗共用了4 500元,求甲、乙两种小鸡苗各购买了多少只?
(2)若购买这批小鸡苗的钱不超过4 700元,问应选购甲种小鸡苗至少多少只?
(3)相关资料表明:甲、乙两种小鸡苗的成活率分别为94%和99%,若要使这批小鸡苗的成活率不低于96%
且买小鸡的总费用最小,问应选购甲、乙两种小鸡苗各多少只?总费用最小是多少元?
相关知识点
推荐套卷
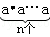 记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
 -4x+2)(
-4x+2)( +8y+16(第二步)
+8y+16(第二步) (第三步)
(第三步)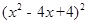 (第四步)
(第四步)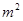 -2m)(
-2m)(
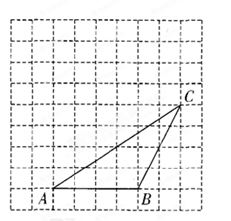
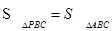 的格点P的个数有 个(点P异于A).
的格点P的个数有 个(点P异于A). 粤公网安备 44130202000953号
粤公网安备 44130202000953号