如图,铁路上A,B两站(视为同一直线上的两点)相距25km,C、D为两村庄(视为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使C,D两村到E站的距离相等且垂直,则E站应建在距A站多少千米处? 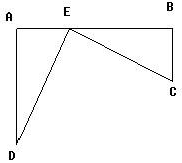
相关知识点
推荐套卷
如图,铁路上A,B两站(视为同一直线上的两点)相距25km,C、D为两村庄(视为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使C,D两村到E站的距离相等且垂直,则E站应建在距A站多少千米处? 