（Ⅰ） 以直角坐标系的原点为极点，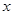
轴的正半轴为极轴，并在两种坐标系中取相同的长度单位已知直线的极坐标方程为
，它与曲线
为参数）相交于两点A和B， 求|AB|;
（Ⅱ）已知极点与原点重合，极轴与x轴正半轴重合，若直线C1的极坐标方程为：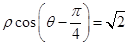
，曲线C2的参数方程为：
（
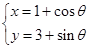为参数），试求曲线C2关于直线C1对称的曲线的直角坐标方程
相关试题
是定义在
上的奇函数，当
时，
，其中
且
．
的不等式
．
，其中
．
的奇偶性；
．
中只有一个元素，求
的值，并把这个元素写出来；
；
，求
的值．
．
在区间（-2，0）内恰有两个零点，求a的取值范围；相关知识点
推荐套卷
（Ⅰ） 以直角坐标系的原点为极点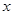，轴的正半轴为极轴，并在两种坐标系中取相同的长度单位已知直线的极坐标方程为，它与曲线为参数）相交于两点A和B， 求|AB|;
（Ⅱ）已知极点与原点重合，极轴与x轴正半轴重合，若直线C1的极坐标方程为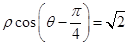：，曲线C2的参数方程为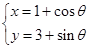：（为参数），试求曲线C2关于直线C1对称的曲线的直角坐标方程
粤公网安备 44130202000953号