如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O.
(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;
(2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.
(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B的两条性质.
相关知识点
推荐套卷
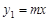 与双曲线
与双曲线 相交于
相交于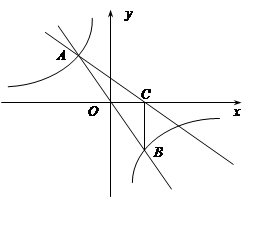
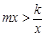 时,
时,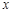 的取值范围.
的取值范围.
 分)商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
分)商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同. 分)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
分)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.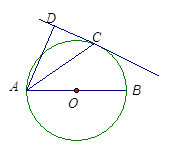
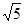 ,求AB的长.
,求AB的长. 粤公网安备 44130202000953号
粤公网安备 44130202000953号