活动探究（本小题满分7分）
如图，已知二次函数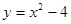
，将
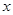轴下方的图象沿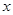轴翻折，得到一个新图象（图中的实线）.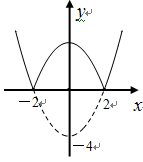
根据新图像回答问题：
（1）当x= ▲ 时，函数y有最小值.
（2）当y随x的增大而增大时，自变量x的范围是 ▲ .
（3）当a＜4时，探究一次函数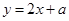
的图像与新图象公共点的个数情况.
,求代数式
的值 .
的方格,作出面积为8平方单位的正方形并涂上阴影,然后在下面的数轴上表示实数
(保留做图痕迹)
的点.(不写作法，保留适当的作图痕迹，要说明理由)
,|-
|,2.3,30%,
,
.相关知识点
推荐套卷
活动探究（本小题满分7分）
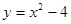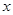如图，已知二次函数，将轴下方的图象沿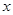轴翻折，得到一个新图象（图中的实线）.
根据新图像回答问题：
（1）当x= ▲ 时，函数y有最小值.
（2）当y随x的增大而增大时，自变量x的范围是 ▲ .
（3）当a＜4时，探究一次函数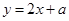的图像与新图象公共点的个数情况.
粤公网安备 44130202000953号