如图,⊙O的圆心在坐标原点,半径为2,直线y=x+b(b>0)与⊙O交于A、B两点,点O关于直线y=x+b的对称点O′,
(1)求证:四边形OAO′B是菱形;
(2)当点O′落在⊙O上时,求b的值.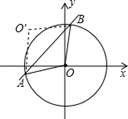
相关知识点
推荐套卷
如图,⊙O的圆心在坐标原点,半径为2,直线y=x+b(b>0)与⊙O交于A、B两点,点O关于直线y=x+b的对称点O′,
(1)求证:四边形OAO′B是菱形;
(2)当点O′落在⊙O上时,求b的值.