已知：在四边形ABCD中，AC = BD，AC与BD交于点O，∠DOC = 60°.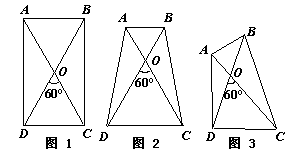
（1）当四边形ABCD是平行四边形时（如图1），证明AB + CD = AC；
（2）当四边形ABCD是梯形时（如图2），AB∥CD，线段AB、CD和线段AC之间的数量关系是_____________________________；
（3）如图3，四边形ABCD中，AB与CD不平行，结论AB + CD = AC是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由.
某人在电车路轨旁与路轨平行的路上骑车行走，他留意到每隔6分钟有一部电车从他后面驶向前面，每隔2分钟有一部电车从对面驶向后面。假设电车和此人行驶的速度都不变（分别为
，
表示），请你根据下面的示意图，求电车每隔几分钟（用t表示）从车站开出一部？
已知：如图（1），⊙O1与⊙O2相交于A、B两点，经过A点的直线分别交⊙O1、⊙O2于C、D两点（C、D不与B重合），连结BD，过点C作BD的平行线交⊙O1于点E，连BE．
（1）求证：BE是⊙O2的切线；
（2）如图（2），若两圆圆心在公共弦AB的同侧，其他条件不变，判断BE和⊙O2的位置关系（不要求证明）．
如图，以等腰三角形ABC的一腰AB为直径的⊙O交底边BC于点D，交AC于点G，连结AD，并过点D作DE⊥AC，垂足为E．根据以上条件写出三个正确结论（除AB=AC,AO=BO,∠ABC=∠ACB外）是：
（1）___________________________________________________________________________；
（2）___________________________________________________________________________；
（3）___________________________________________________________________________．
如图所示，已知△ABC中，AC=BC=6，∠C=90°．O是AB的中点，⊙O与AC相切于点D、与BC相切于点E．设⊙O交OB于F，连DF并延长交CB的延长线于G．
（1）∠BFG与∠BGF是否相等?为什么?
（2）求由DG、GE和
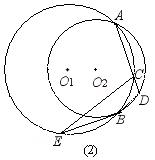
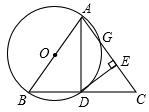
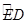所围成的图形的面积（阴影部分）．
粤公网安备 44130202000953号