如图,在圆内画 条线段,将圆分割成两部分;画
条线段,将圆分割成两部分;画 条相交线段,彼此分割成
条相交线段,彼此分割成 条线段,将圆分割成
条线段,将圆分割成 部分;画
部分;画 条线段,彼此最多分割成
条线段,彼此最多分割成 条线段,将圆最多分割成
条线段,将圆最多分割成 部分;画
部分;画 条线段,彼此最多分割成
条线段,彼此最多分割成 条线段,将圆最多分割成
条线段,将圆最多分割成 部分.
部分.



(1)猜想:圆内两两相交的 条线段,彼此最多分割成多少条线段?
条线段,彼此最多分割成多少条线段?
(2)记在圆内画 条线段,将圆最多分割成
条线段,将圆最多分割成 部分,归纳出
部分,归纳出 与
与 的关系.
的关系.
(3)猜想数列 的通项公式,根据
的通项公式,根据 与
与 的关系及数列的知识,证明你的猜想是否成立.
的关系及数列的知识,证明你的猜想是否成立.
相关知识点
推荐套卷
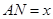 米,花坛AMPN的面积为
米,花坛AMPN的面积为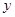 平方米
平方米
 的函数解析式和定义域;
的函数解析式和定义域;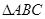 中,
中,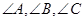 所对的边分别为
所对的边分别为 ,已知
,已知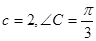
 ,求
,求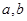 的值;
的值; 的最大值.
的最大值.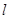 过点(1,2)且在x,y轴上的截距相等
过点(1,2)且在x,y轴上的截距相等 在直线
在直线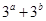 的最小值.
的最小值. 中,底面
中,底面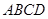 为菱形,
为菱形,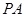 ⊥平面
⊥平面 交
交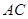 于点
于点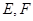 是线段
是线段 中点,
中点, 为线段
为线段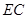 中点.
中点.
 //平面
//平面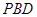 ;
;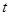 (天)的函数,且销售量近似满足
(天)的函数,且销售量近似满足 (件),价格近似满足
(件),价格近似满足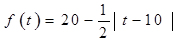 (元).
(元).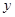 与时间
与时间 )的函数关系表达式;
)的函数关系表达式; 粤公网安备 44130202000953号
粤公网安备 44130202000953号